Lecture 19 - Transformers#
Learning goals#
Define tokens, embeddings, positional encodings, attention, and multi-head attention.
Visualize attention as heatmaps on SMILES examples.
Implement a mini Transformer Encoder block and train it on a chemistry task from SMILES.
1. Setup#
1. From SMILES to tokens#
We will treat a SMILES string as a sequence of characters. This is not the only way to tokenize chemistry, but it is simple and enough for a first pass.
Token: a symbol in a sequence. Here we use characters such as
C,O,(,),=, digits for ring closures, and[]for special atoms.Embedding: a vector that represents a token.
Sequence length: number of tokens.
# Build a tiny SMILES vocabulary from a small set of molecules
sample_smiles = [
"CCO", # ethanol
"CC(=O)O", # acetic acid
"c1ccccc1", # benzene
"CCN", # ethylamine
"CCCl", # chloroethane
"CC(=O)NC", # acetamide
"C=CC=O", # acrolein
"C1CCCCC1", # cyclohexane
]
# Extract characters seen in these SMILES plus a few common brackets
special = list("[]=#@+-")
chars = sorted(set("".join(sample_smiles)) | set(special) | set("()"))
# Add PAD and UNK
itos = ["<PAD>", "<UNK>"] + chars
stoi = {ch:i for i,ch in enumerate(itos)}
print("Vocab size:", len(itos))
print("First 20 tokens:", itos[:20])
def tokenize(smiles, max_len=24):
ids = []
for ch in smiles:
ids.append(stoi.get(ch, stoi["<UNK>"]))
# pad or trim
ids = ids[:max_len] + [stoi["<PAD>"]] * max(0, max_len - len(ids))
return np.array(ids, dtype=np.int64)
def detokenize(ids):
return "".join([itos[i] if 0 <= i < len(itos) else "?" for i in ids if itos[i] != "<PAD>"])
x = tokenize("CC(=O)O", max_len=16)
print("Token ids for acetic acid:", x[:10], "...")
print("Back to text:", detokenize(x))
Vocab size: 17
First 20 tokens: ['<PAD>', '<UNK>', '#', '(', ')', '+', '-', '1', '=', '@', 'C', 'N', 'O', '[', ']', 'c', 'l']
Token ids for acetic acid: [10 10 3 8 12 4 12 0 0 0] ...
Back to text: CC(=O)O
Now we will load the C-H oxidation dataset with SMILES and properties.
# Load data
url = "https://raw.githubusercontent.com/zzhenglab/ai4chem/main/book/_data/C_H_oxidation_dataset.csv"
df_raw = pd.read_csv(url)
print("Columns:", list(df_raw.columns))
df_raw.head(3)
def calc_descriptors(smiles):
if Chem is None:
return pd.Series({"MolWt": np.nan, "LogP": np.nan, "TPSA": np.nan, "NumRings": np.nan})
m = Chem.MolFromSmiles(smiles)
if m is None:
return pd.Series({"MolWt": np.nan, "LogP": np.nan, "TPSA": np.nan, "NumRings": np.nan})
return pd.Series({
"MolWt": Descriptors.MolWt(m),
"LogP": Crippen.MolLogP(m),
"TPSA": rdMolDescriptors.CalcTPSA(m),
"NumRings": rdMolDescriptors.CalcNumRings(m),
})
desc = df_raw["SMILES"].apply(calc_descriptors)
df = pd.concat([df_raw, desc], axis=1)
# Build classification frame
label_map = {"toxic": 1, "non_toxic": 0}
df_clf = df.dropna(subset=["SMILES"]).copy()
df_clf = df_clf[df_clf["Toxicity"].str.lower().isin(label_map.keys())]
df_clf["y"] = df_clf["Toxicity"].str.lower().map(label_map).astype(int)
print("Class balance:\n", df_clf["y"].value_counts())
df_clf.head(3)
Columns: ['Compound Name', 'CAS', 'SMILES', 'Solubility_mol_per_L', 'pKa', 'Toxicity', 'Melting Point', 'Reactivity', 'Oxidation Site']
Class balance:
y
1 474
0 101
Name: count, dtype: int64
| Compound Name | CAS | SMILES | Solubility_mol_per_L | pKa | Toxicity | Melting Point | Reactivity | Oxidation Site | MolWt | LogP | TPSA | NumRings | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3,4-dihydro-1H-isochromene | 493-05-0 | c1ccc2c(c1)CCOC2 | 0.103906 | 5.80 | non_toxic | 65.8 | 1 | 8,10 | 134.178 | 1.7593 | 9.23 | 2.0 | 0 |
| 1 | 9H-fluorene | 86-73-7 | c1ccc2c(c1)Cc1ccccc1-2 | 0.010460 | 5.82 | toxic | 90.0 | 1 | 7 | 166.223 | 3.2578 | 0.00 | 3.0 | 1 |
| 2 | 1,2,3,4-tetrahydronaphthalene | 119-64-2 | c1ccc2c(c1)CCCC2 | 0.020589 | 5.74 | toxic | 69.4 | 1 | 7,10 | 132.206 | 2.5654 | 0.00 | 2.0 | 1 |
2. Embeddings and positional encoding#
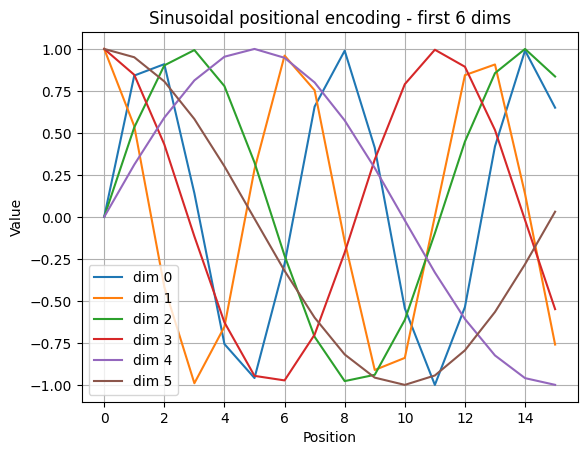
We map each token id to a vector of size d_model. We also add a position-dependent signal so the model can tell the difference between the same token at different positions.
Embeddings and positions
For token id \(x_t\) and model size \(d\):
$\(
E_t = W_{\text{emb}}[x_t] \in \mathbb{R}^{d}
\)\(
Sinusoidal positional encoding for position \)p\( and channels \)2i, 2i+1\(:
\)\(
\text{PE}(p,2i) = \sin\!\left(\frac{p}{10000^{2i/d}}\right),\quad
\text{PE}(p,2i+1) = \cos\!\left(\frac{p}{10000^{2i/d}}\right)
\)\(
Input to attention is \)H_t = E_t + \text{PE}_t$.
def sinusoidal_positional_encoding(seq_len, d_model):
pe = np.zeros((seq_len, d_model), dtype=np.float32)
for pos in range(seq_len):
for i in range(0, d_model, 2):
denom = 10000 ** (i / d_model)
pe[pos, i] = math.sin(pos / denom)
if i + 1 < d_model:
pe[pos, i + 1] = math.cos(pos / denom)
return pe
# Example
seq_len = 16
d_model = 32
pe = sinusoidal_positional_encoding(seq_len, d_model)
print_shape("pe", pe)
# Visualize a few dimensions
plt.figure()
for d in [0, 1, 2, 3, 4, 5]:
plt.plot(pe[:40, d], label=f"dim {d}")
plt.title("Sinusoidal positional encoding - first 6 dims")
plt.xlabel("Position")
plt.ylabel("Value")
plt.legend()
plt.grid(True)
plt.show()
pe.shape = (16, 32)
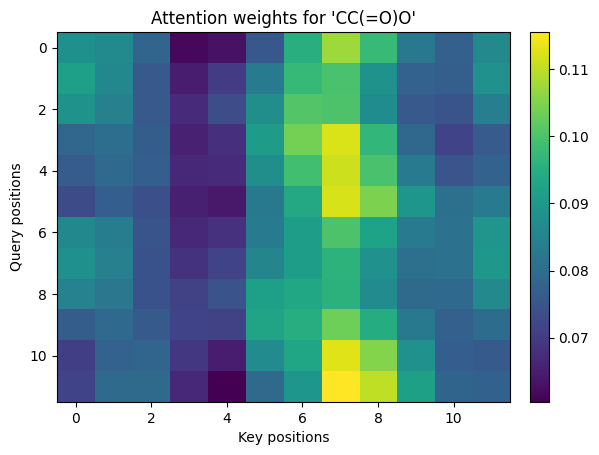
3. Scaled dot-product attention#
Given query Q, key K, and value V, attention is:
def softmax_np(x, axis=-1):
x = x - np.max(x, axis=axis, keepdims=True)
e = np.exp(x)
return e / np.sum(e, axis=axis, keepdims=True)
def scaled_dot_product_attention_np(Q, K, V, mask=None):
d_k = Q.shape[-1]
scores = Q @ K.transpose(0,2,1) / math.sqrt(d_k) # (B, Tq, Tk)
if mask is not None:
scores = scores + (mask * -1e9)
weights = softmax_np(scores, axis=-1)
out = weights @ V
return out, weights
# Build toy embeddings by projecting one-hot tokens
def one_hot(vocab_size, ids):
oh = np.zeros((len(ids), vocab_size), dtype=np.float32)
for i, idx in enumerate(ids):
if idx < vocab_size:
oh[i, idx] = 1.0
return oh
rng = np.random.default_rng(0)
d_model = 16
max_len = 12
sm = "CC(=O)O"
ids = tokenize(sm, max_len=max_len)
T = len(ids)
E = rng.standard_normal((len(itos), d_model)).astype(np.float32) * 0.1 # embedding table
X = one_hot(len(itos), ids) @ E # (T, d_model)
PE = sinusoidal_positional_encoding(max_len, d_model)
H = X + PE[:T] # add position
# Linear projections
Wq = rng.standard_normal((d_model, d_model)).astype(np.float32) * 0.2
Wk = rng.standard_normal((d_model, d_model)).astype(np.float32) * 0.2
Wv = rng.standard_normal((d_model, d_model)).astype(np.float32) * 0.2
Q = H @ Wq
K = H @ Wk
V = H @ Wv
# Add batch dimension B=1
Qb = Q[None, ...]
Kb = K[None, ...]
Vb = V[None, ...]
out, weights = scaled_dot_product_attention_np(Qb, Kb, Vb)
print_shape("Q", Qb); print_shape("K", Kb); print_shape("V", Vb)
print_shape("weights", weights); print_shape("out", out)
# Visualize attention weights
show_img(weights[0], title=f"Attention weights for '{sm}'")
Q.shape = (1, 12, 16)
K.shape = (1, 12, 16)
V.shape = (1, 12, 16)
weights.shape = (1, 12, 12)
out.shape = (1, 12, 16)
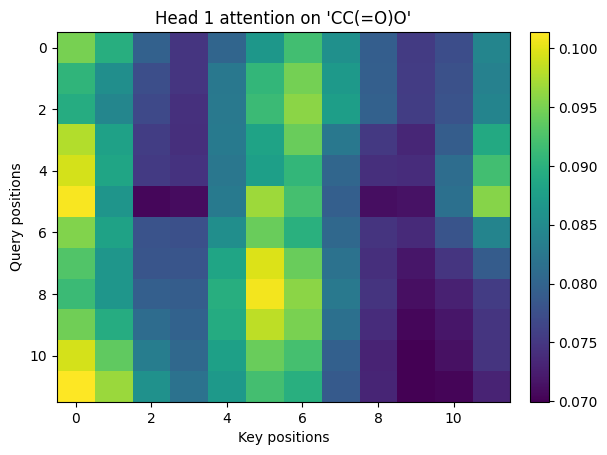
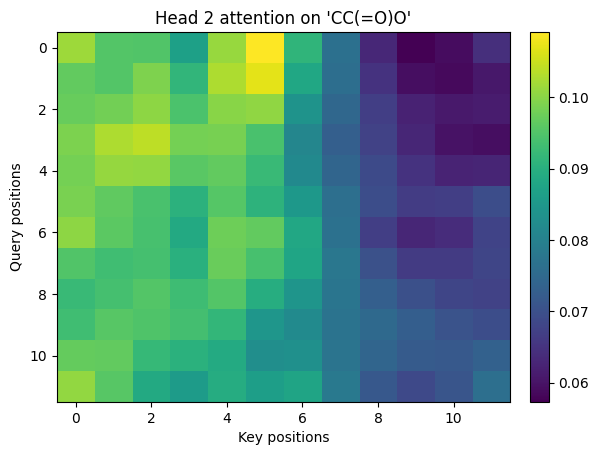
4. Multi-head attention#
Multiple heads split the model dimension into smaller subspaces that attend differently. We will build 2 heads for clarity.
Multi-head attention with \(h\) heads have the following equation:
$\(
\text{MHA}(X) = \text{Concat}(\text{head}_1,\dots,\text{head}_h)W^O,\quad
\text{head}_j = \text{Attn}(XW_j^Q, XW_j^K, XW_j^V)
\)$
Later, we will build Residual and LayerNorm:
$\(
Y = \text{LayerNorm}(X + \text{SubLayer}(X))
\)$
with Classifier head:
$\(
\hat{y} = \text{softmax}(W_c\, \text{Pool}(H) + b_c)
\)$
and Losses:
$\(
\mathcal{L}_{\text{CE}} = -\frac{1}{N}\sum_{i=1}^N\sum_{c=1}^2 y_{i,c}\log \hat{p}_{i,c}
\qquad
\text{MSE} = \frac{1}{N}\sum_i (y_i - \hat{y}_i)^2
\)$
def multi_head_attention_np(H, num_heads=2):
B = 1
T, d_model = H.shape
assert d_model % num_heads == 0
d_k = d_model // num_heads
rng = np.random.default_rng(1)
Wq = rng.standard_normal((num_heads, d_model, d_k)).astype(np.float32) * 0.2
Wk = rng.standard_normal((num_heads, d_model, d_k)).astype(np.float32) * 0.2
Wv = rng.standard_normal((num_heads, d_model, d_k)).astype(np.float32) * 0.2
Wo = rng.standard_normal((num_heads * d_k, d_model)).astype(np.float32) * 0.2
all_weights = []
all_heads = []
for h in range(num_heads):
Q = H @ Wq[h]
K = H @ Wk[h]
V = H @ Wv[h]
out, w = scaled_dot_product_attention_np(Q[None, ...], K[None, ...], V[None, ...])
all_weights.append(w[0])
all_heads.append(out[0])
H_cat = np.concatenate(all_heads, axis=-1) # (T, num_heads*d_k)
Y = H_cat @ Wo # (T, d_model)
return Y, all_weights
Y, head_weights = multi_head_attention_np(H, num_heads=2)
print_shape("Y (mha output)", Y)
# Visualize each head
for i, w in enumerate(head_weights, 1):
show_img(w, title=f"Head {i} attention on '{sm}'")
Y (mha output).shape = (12, 16)
5. Transformer Encoder block for a small chemistry task#
Now, we will use what we learn before to do a demo.
We train a small encoder on SMILES to predict toxic vs non_toxic.
In the section, we will:
Split the data with stratification
Create a character vocab, tokenizer, and padding policy
Build a
DatasetandDataLoaderwith a custom collateDefine a tiny encoder with sinusoidal positional encoding and mean pooling
Train with cross entropy and track loss
Report accuracy and ROC AUC, draw a confusion matrix and an ROC curve
Inspect one attention head on a test sequence
import random
SEED = 42
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
# Split
X_text = df_clf['SMILES'].astype(str).tolist()
y_all = df_clf['y'].values.astype(np.int64)
X_train_txt, X_test_txt, y_train, y_test = train_test_split(
X_text, y_all, test_size=0.2, random_state=SEED, stratify=y_all
)
print(f"Train size: {len(X_train_txt)} Test size: {len(X_test_txt)}")
Train size: 460 Test size: 115
We use a simple character vocab built from the training SMILES. A special pad token fills sequences to a common length.
Let \( S \) be the set of non pad positions for a sequence with hidden states \( h_t \in \mathbb{R}^{d} \).
Mean pooling over valid tokens:
$\(
\bar{h} \;=\; \frac{1}{|S|}\sum_{t \in S} h_t
\)$
Sinusoidal positional encoding for position (p) and channel index (2i) and (2i+1): $\( \mathrm{PE}(p, 2i) = \sin\!\left(p \,/\, 10000^{\frac{2i}{d}}\right), \quad \mathrm{PE}(p, 2i+1) = \cos\!\left(p \,/\, 10000^{\frac{2i}{d}}\right). \)$
# Specials and vocab
PAD_TOKEN = "<pad>"
UNK_TOKEN = "<unk>"
MAX_LEN = 256 # keep this in sync with the model
# Build vocab from training texts
chars = sorted(set("".join(X_train_txt)))
itos = [PAD_TOKEN, UNK_TOKEN] + chars
stoi = {t: i for i, t in enumerate(itos)}
PAD = stoi[PAD_TOKEN]
UNK = stoi[UNK_TOKEN]
def tokenize(s: str):
ids = [stoi.get(ch, UNK) for ch in s]
return ids[:MAX_LEN]
def sinusoidal_positional_encoding(max_len: int, d_model: int):
pe = np.zeros((max_len, d_model), dtype=np.float32)
position = np.arange(max_len)[:, None]
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
pe[:, 0::2] = np.sin(position * div_term)
pe[:, 1::2] = np.cos(position * div_term)
return pe
# Dataset and collate
class SmilesSet(Dataset):
def __init__(self, texts, labels):
self.texts = texts
self.labels = labels
def __len__(self):
return len(self.texts)
def __getitem__(self, idx):
ids = tokenize(self.texts[idx])
return np.array(ids, dtype=np.int64), int(self.labels[idx])
def collate(batch):
xs, ys = zip(*batch)
max_len = max(len(x) for x in xs)
pad_x = [np.pad(x, (0, max_len - len(x)), constant_values=PAD) for x in xs]
return torch.from_numpy(np.stack(pad_x)).long(), torch.tensor(ys).long()
train_ds = SmilesSet(X_train_txt, y_train)
test_ds = SmilesSet(X_test_txt, y_test)
train_loader = DataLoader(train_ds, batch_size=64, shuffle=True, collate_fn=collate)
test_loader = DataLoader(test_ds, batch_size=256, shuffle=False, collate_fn=collate)
print(f"Vocab size: {len(itos)} tokens")
Vocab size: 36 tokens
Now, we use a tiny Transformer encoder with multi head self attention and a feed forward block, then mean pooling and a classifier head.
Binary cross entropy over softmax probabilities reduces to the usual cross entropy on two classes: $\( L \;=\; -\frac{1}{N}\sum_{i=1}^{N} \sum_{c \in \{0,1\}} y_{ic}\,\log p_{ic}. \)$
# Tiny transformer encoder
class TinyEncoder(nn.Module):
def __init__(self, vocab, d_model=64, heads=2, ff=128, max_len=256):
super().__init__()
self.emb = nn.Embedding(vocab, d_model, padding_idx=PAD)
pe = sinusoidal_positional_encoding(max_len, d_model).astype(np.float32)
self.register_buffer("pe", torch.from_numpy(pe))
self.mha = nn.MultiheadAttention(d_model, heads, batch_first=True)
self.ln1 = nn.LayerNorm(d_model)
self.ff = nn.Sequential(
nn.Linear(d_model, ff),
nn.ReLU(),
nn.Linear(ff, d_model),
)
self.ln2 = nn.LayerNorm(d_model)
self.cls = nn.Sequential(
nn.Linear(d_model, d_model),
nn.ReLU(),
nn.Linear(d_model, 2)
)
def forward(self, x):
B, T = x.shape
h = self.emb(x) + self.pe[:T].unsqueeze(0)
key_padding = (x == PAD) # True positions are ignored
h2, attn = self.mha(h, h, h, key_padding_mask=key_padding, need_weights=True, average_attn_weights=False)
h = self.ln1(h + h2)
h2 = self.ff(h)
h = self.ln2(h + h2)
# mean pool over valid tokens
denom = (~key_padding).sum(dim=1, keepdim=True).clamp(min=1)
pooled = (h.masked_fill(key_padding.unsqueeze(-1), 0).sum(dim=1) / denom)
logits = self.cls(pooled)
return logits, attn, key_padding
device = "cuda" if torch.cuda.is_available() else "cpu"
model = TinyEncoder(len(itos), d_model=64, heads=2, ff=128, max_len=MAX_LEN).to(device)
opt = torch.optim.AdamW(model.parameters(), lr=3e-3, weight_decay=1e-4)
def run_epoch(loader, train=True):
if train: model.train()
else: model.eval()
total, correct, losses = 0, 0, []
for xb, yb in loader:
xb, yb = xb.to(device), yb.to(device)
logits, _, _ = model(xb)
loss = F.cross_entropy(logits, yb)
if train:
opt.zero_grad()
loss.backward()
opt.step()
pred = logits.argmax(dim=1)
correct += (pred == yb).sum().item()
total += yb.size(0)
losses.append(loss.item())
return np.mean(losses), correct / max(total, 1)
# Train
epochs = 15
history = []
for ep in range(epochs):
tr_loss, tr_acc = run_epoch(train_loader, train=True)
te_loss, te_acc = run_epoch(test_loader, train=False)
history.append((tr_loss, tr_acc, te_loss, te_acc))
if (ep + 1) % 5 == 0:
print(f"epoch {ep+1:02d} train_loss={tr_loss:.4f} train_acc={tr_acc:.3f} test_acc={te_acc:.3f}")
# Plot training curve
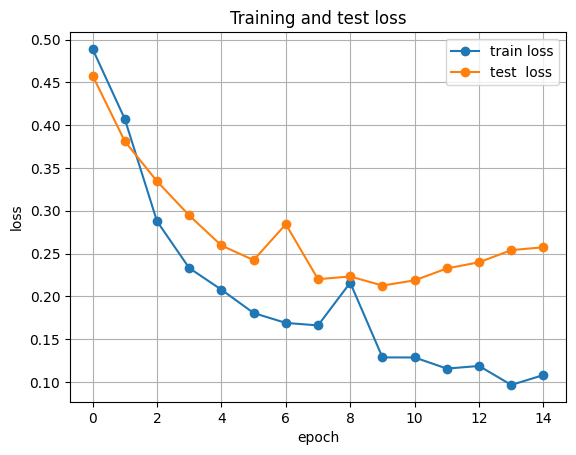
plt.figure()
plt.plot([h[0] for h in history], label="train loss", marker="o")
plt.plot([h[2] for h in history], label="test loss", marker="o")
plt.xlabel("epoch")
plt.ylabel("loss")
plt.title("Training and test loss")
plt.grid(True)
plt.legend()
plt.show()
epoch 05 train_loss=0.2077 train_acc=0.900 test_acc=0.896
epoch 10 train_loss=0.1285 train_acc=0.930 test_acc=0.913
epoch 15 train_loss=0.1079 train_acc=0.941 test_acc=0.930
# Final evaluation
model.eval()
probs, y_true, y_pred = [], [], []
with torch.no_grad():
for xb, yb in test_loader:
logits, _, _ = model(xb.to(device))
p = F.softmax(logits, dim=1)[:, 1].cpu().numpy()
probs.extend(p.tolist())
y_true.extend(yb.numpy().tolist())
y_pred.extend(logits.argmax(dim=1).cpu().numpy().tolist())
acc = accuracy_score(y_true, y_pred)
try:
auc = roc_auc_score(y_true, probs)
except Exception:
auc = float("nan")
print(f"Test accuracy: {acc:.3f}")
print(f"Test ROC AUC: {auc:.3f}")
print(classification_report(y_true, y_pred, digits=3))
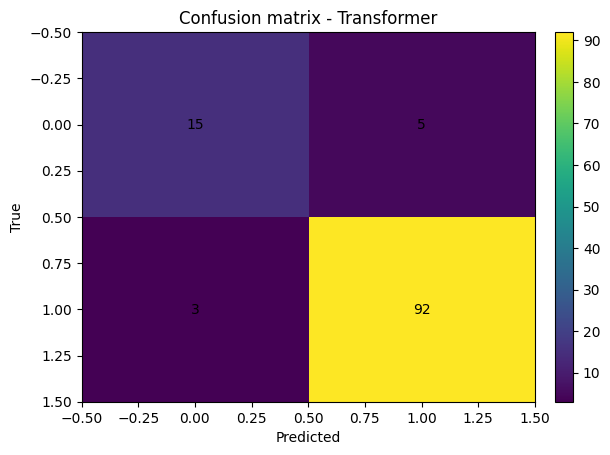
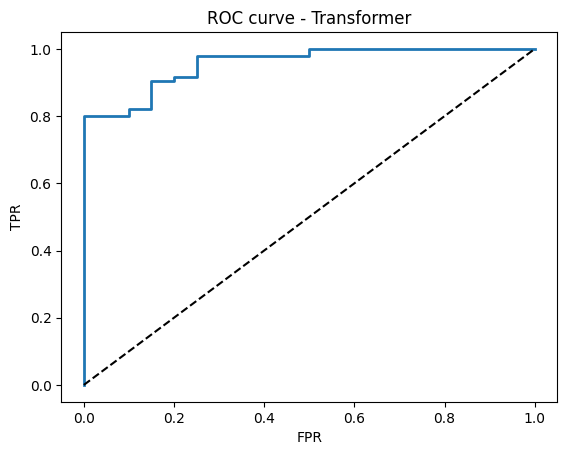
Test accuracy: 0.930
Test ROC AUC: 0.957
precision recall f1-score support
0 0.833 0.750 0.789 20
1 0.948 0.968 0.958 95
accuracy 0.930 115
macro avg 0.891 0.859 0.874 115
weighted avg 0.928 0.930 0.929 115
Below we will plot the results:
# Confusion matrix
cm = confusion_matrix(y_true, y_pred)
plt.figure()
plt.imshow(cm, aspect="auto")
plt.title("Confusion matrix - Transformer")
plt.xlabel("Predicted")
plt.ylabel("True")
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
plt.text(j, i, cm[i, j], ha="center", va="center")
plt.colorbar(fraction=0.046, pad=0.04)
plt.show()
# ROC curve
try:
fpr, tpr, thr = roc_curve(y_true, probs)
plt.figure()
plt.plot(fpr, tpr, lw=2)
plt.plot([0, 1], [0, 1], "k--")
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.title("ROC curve - Transformer")
plt.show()
except Exception as e:
print("ROC not available:", e)
# Attention peek
def show_img(M, title=""):
plt.figure()
plt.imshow(M, aspect="auto")
plt.title(title)
plt.xlabel("Key positions")
plt.ylabel("Query positions")
plt.colorbar(fraction=0.046, pad=0.04)
plt.show()
# one batch
xb, yb = next(iter(test_loader))
with torch.no_grad():
logits, attn, padmask = model(xb.to(device))
# attn shape handling
if isinstance(attn, torch.Tensor):
if attn.dim() == 4: # (B, heads, T, S)
head0 = attn[0, 0].cpu().numpy()
elif attn.dim() == 3: # (heads, T, S)
head0 = attn[0].cpu().numpy()
else:
head0 = attn.mean(0).cpu().numpy()
else:
# unknown object, skip
head0 = None
if head0 is not None:
seq_ids = xb[0].numpy()
tok_str = [itos[i] for i in seq_ids if i != PAD]
T = len(tok_str)
show_img(head0[:T, :T], title="Head 1 attention on a test SMILES")
print("Tokens:", tok_str[:40])
else:
print("Could not parse attention weights.")
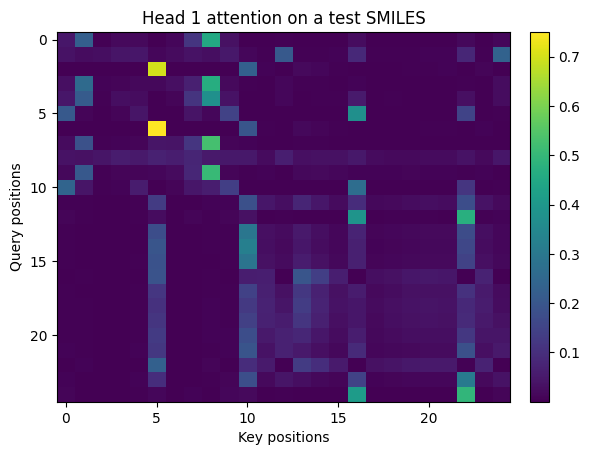
Tokens: ['O', '=', 'C', '(', 'O', ')', 'C', '(', '=', 'O', ')', 'c', '1', 'c', 'c', 'c', '2', 'c', 'c', 'c', 'c', 'c', '2', 'c', '1']
6. Glossary#
- Token #
a basic symbol in a sequence. We use characters from SMILES.
- Embedding#
a learned vector for each token.
- Positional encoding#
a vector added to embeddings so the model knows token order.
- Query, Key, Value (Q, K, V)#
linear projections of hidden states used in attention.
- Attention weights#
softmax scores that say how much each position attends to others.
- Head#
one set of Q, K, V projections inside multi-head attention.
- Residual connection#
add input of a block to its output for stable optimization.
- LayerNorm#
normalization per token over channels.
- Cross entropy #
a loss for classification.

